As ever, wikipedia gives an excellent starting point here .
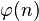 or phi(n) is defined as the number of natural numbers less than or equal to n and are coprime to n.
or phi(n) is defined as the number of natural numbers less than or equal to n and are coprime to n.
phi(4) = 2 (The numbers 1 and 3)
phi(12) = 4 (The numbers 1, 5, 7 and 11)
phi(13) = 12 (All numbers below 13)
In general phi(p) = p-1 when is a prime.
Generalising further, when N = paqbrc
phi(N) = N (1-1/p) * (1-1/q) * (1-1/r) (The proof for this is intuitive enough. Keep eliminating all numbers that are not coprime from 1 to N-1)
Now, Euler's phi function states this
For two numbers m,n that are coprime (HCF of m,n =1)
m phi(n) = 1 mod n, (m phi(n) leaves a remainder of 1 when divided by n)
m phi(n) – 1 is a multiple of n
When we apply it in a scenario where n is prime, we get
m p-1 = 1 mod p
m p-1 – 1 is a multiple of n
This last observation is also called Fermat's Little Theorem . In many ways, Euler's phi function is an extension of Fermat's Little Theorem.
Excellent theorem, fairly clear implications whenever a question on remainders is asked. For instance if a question states What is the remainder when 100^56 is divided by 29, we can straight away see that the answer is 1. Having said that, I do not think that a CAT question will require students to know Euler's phi function and properties. Any question that gets simplified using Euler's phi function will have a simpler alternate solution as well. Even if you solve using Euler's phi function, kindly look for the alternate method.
The proof for Euler's Phi function and/or Fermat's Little Theorem can be found here.
The proof for Wilson's Theorem can be seen here.
The proof for Wilson's Theorem can be seen here.